GNN Part 1 - 教師なし頂点表現学習問題
本記事からしばらくの間, 「グラフニューラルネットワーク」佐藤竜馬 著を教科書としてGNNの基礎について学んでいきます.
本記事では, 「グラフニューラルネットワーク」Chapter2.3 古典的なグラフ機械学習手法において紹介されている教師なし頂点表現学習問題を, JAXを用いて実装してみます. なお, 今回実装したコードはGitHubにて公開しています.
目次:
教師なし頂点表現学習問題
教師なし頂点表現学習問題は以下のような問題です.
- 入力: 重み付きグラフ $G = (V, E, w)$ ($V$は頂点集合, $E$は辺集合, $w$は辺の重み)
- 出力: グラフ構造を考慮した頂点の埋め込み $Z \in \mathbb{R}^{n \times d}$ ($n$は頂点数, $d$は埋め込み次元)
この問題は, グラフ構造を考慮した頂点の埋め込みを学習する問題です.
埋め込みとはデータの情報を低次元のベクトルに変換したもので, 機械学習においてデータの特徴を扱いやすいベクトルとして抽出するために用いられます. 自然言語処理においては単語の埋め込み(Word Embedding)が有名です. 今回はそのグラフ版です.
この問題の出力として得られる$Z$は, 各行$Z_i$が頂点$i$の埋め込みベクトルとなります. よって, $Z$を求めることで, グラフデータを, 扱いやすいベクトルデータに変換し, 機械学習の問題に持ってくることができます.
ただ, “グラフ構造を考慮した”という部分が曖昧です. ここでは, 教師なし頂点表現学習問題を以下の最適化問題として定式化することで, グラフ構造を考慮した頂点の埋め込みを学習します.
\[\min_{Z\in \mathbb{R}^{n \times d}} \frac{1}{2} \sum_{u\in V} \sum_{v\in V}((D_{uv} + W_{uv})-Z_u^T Z_v)^2\]ここで, $D \in \mathbb{R}^{n \times n}$は次数行列, $W \in \mathbb{R}^{n \times n}$は隣接行列です. 次数行列は各頂点の次数を対角成分に持つ行列で, 隣接行列は隣接する頂点間の重みを持つ行列です.
この最適化問題は, $Z_u^T Z_v$が$D_{uv} + W_{uv}$に近づくように$Z$を学習する問題です. 各頂点$u$の埋め込みベクトルは$Z_u$であることから, この最適化問題は, 隣接している頂点同士の埋め込みベクトルの内積が大きくなるように設計されています.
最適化問題の求め方
教師なし頂点表現学習問題の最適化問題は, 「グラフニューラルネットワーク」では行列分解を用いて解く方法が紹介されています.
今回は, JAXを用いて, 勾配降下法及び行列分解で最適化問題を解くコードを装してみます.
具体例として, 以下のグラフを用います.
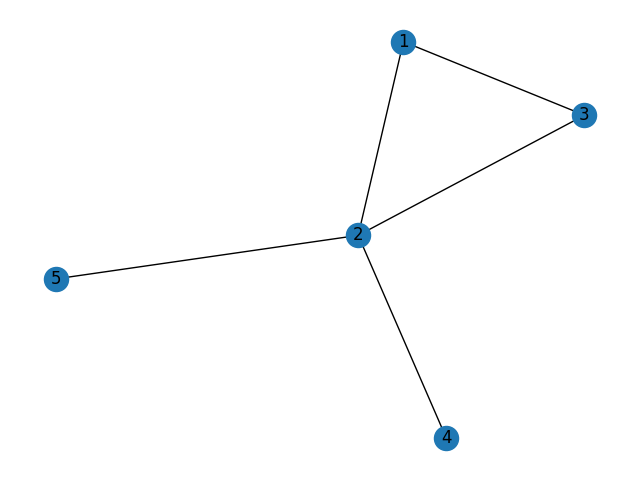
このグラフの次数行列$D$と隣接行列$W$は以下の通りです.
D = jnp.diag(jnp.array([2, 4, 2, 1, 1]))
print("D", D)
# [[2 0 0 0 0]
# [0 4 0 0 0]
# [0 0 2 0 0]
# [0 0 0 1 0]
# [0 0 0 0 1]]
# adjacency matrix
W = jnp.array([
[0, 1, 1, 0, 0],
[1, 0, 1, 1, 1],
[1, 1, 0, 0, 0],
[0, 1, 0, 0, 0],
[0, 1, 0, 0, 0]
])
この時の正解データである, $D + W$は以下のような行列になります.
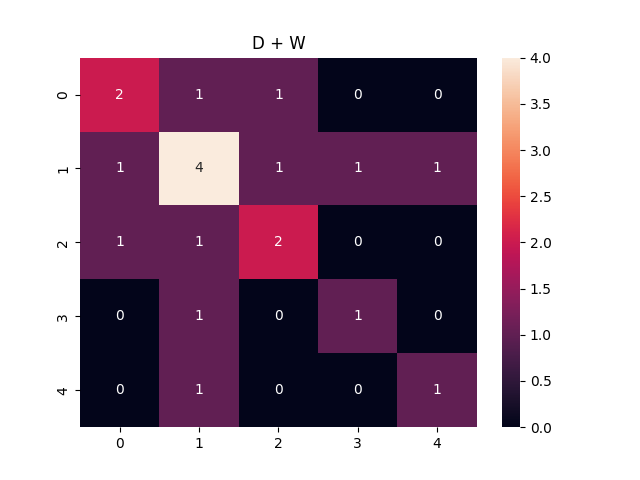
$Z$は, $Z@Z.T$が$D+W$に近づくように学習されます.
勾配降下法による求解
勾配降下法では, パラメータ$Z$をランダムに初期化し, $D+W$と$Z@Z.T$の差を最小化するようにパラメータ$Z$を更新していきます.
まず, 最適化問題を解くための損失関数を定義します.
def loss_fn(Z):
loss = 0
#愚直な方法
#for u in range(5):
# for v in range(5):
# loss += ((D[u,v] + W[u,v]) - Z[u].T @ Z[v])**2
# 行列演算を用いた方法
loss = jnp.sum((D + W - Z @ Z.T)**2)
return loss
続いて, 勾配降下法のupdate関数を定義します.
def update(theta, lr=0.01):
loss, grad = jax.value_and_grad(loss_fn)(theta)
return theta - lr * grad, loss
最後に, 勾配降下法で最適化問題を解きます.
Z = jax.random.uniform(key = jax.random.PRNGKey(0), shape=(D.shape[0], d))
for epoch in range(1000):
Z, loss = update(Z)
if epoch % 10 == 0:
print(f"Epoch {epoch}, Loss {loss}")
行列分解による求解
「グラフニューラルネットワーク」でも紹介されているように, 今回の最適化問題は行列分解によって最適解が求められます. 実装は以下のようにして行えます.
e, V = jnp.linalg.eigh(D + W)
Z = jnp.zeros((D.shape[0], d))
for i in range(min(d, D.shape[0])):
Z = Z.at[:,i].set(V[:, -1 - i] * jnp.sqrt(e[-1 - i]))
導出方法については, 教科書を参照ください.
結果
埋め込み次元d=5の場合
埋め込み次元$d = 5$ としたときのZのheatmapは以下の通りです.
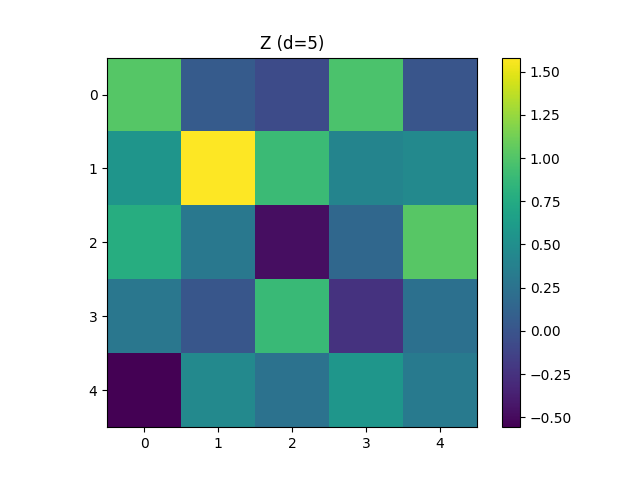
これだけ見てもよくわからないので, 埋め込みベクトル同士の内積$Z @ Z.T$のheatmapを見てみます.
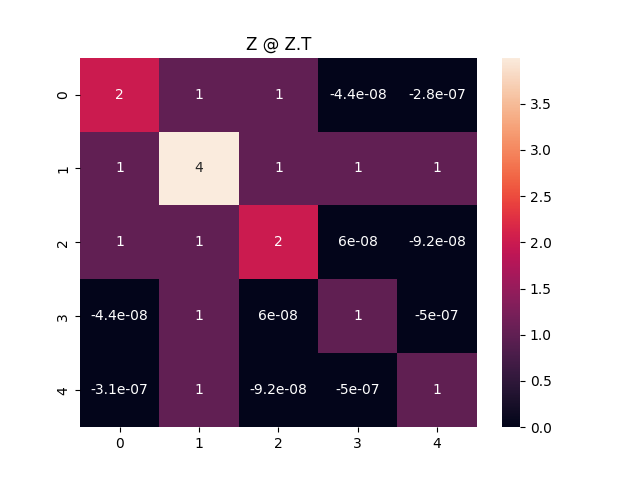
正解データである$D+W$とほとんど同じ行列であることがわかります. よって, 正しく埋め込みベクトルが学習できていることがわかります.
行列分解による最適解も見てみましょう. 以下に$Z$と$Z@Z.T$のheatmapを示します.
 |
 |
$Z$は勾配降下法で得られた解と行列分解で得られた解で大きく異なっていますが, $Z@Z.T$はどちらも正解データである$D+W$とほとんど同じ値が得られました. これは, $d=5$の場合, 最適解が複数存在することを示しています.
埋め込み次元dを変えてみる
埋め込み次元$d \in {3, 10}$にした時の, 勾配降下法, 行列分解で計算した$Z$, $Z@Z.T$を見てみましょう.
- d=3
 |
 |
 |
 |
$d=3$の時は, どちらの方法でも, 情報が圧縮されるため正解データとの誤差が大きくなります. しかし, 行列分解により得られた解は最適解となるため, 局所解に陥る可能性のある勾配降下法に比べて誤差が小さいです.
- d=10
 |
 |
 |
 |
$d=10$の場合は, どちらの方法でも$Z@Z.T$が正解データとほぼ等しくなっており, 最適解が得られています.
面白いポイントは, 行列分解で得られた解はアルゴリズムから当たり前ですが$Z[:,n+1]$以降の値が0になっていることです.
まとめ
教師なし頂点表現学習問題を勾配降下法と行列分解によって解く方法を実装しました. 教師なし頂点表現学習問題を最適化問題に落とし込むことで埋め込み表現を簡単に得られるため, 面白いと感じました.
今回の最適化問題は以下のような定式化でしたが, 損失の設計を変えることで多様な埋め込み表現を得ることができるそうです.
\[\min_{Z\in \mathbb{R}^{n \times d}} \frac{1}{2} \sum_{u\in V} \sum_{v\in V}((D_{uv} + W_{uv})-Z_u^T Z_v)^2\]参考文献
- グラフニューラルネットワーク, 佐藤竜馬 著, 講談社, 2024
- Word embedding, Wikipedia, https://en.wikipedia.org/wiki/Word_embedding
- 実装コード: https://github.com/speed1313/gnnbook/tree/main/src/gnnbook/prop2-3